
论文标题:数据驱动-物理指引的神经网络求解中子扩散方程特征值问题的不确定性分析
论文作者:杨宇,龚禾林*,贺巧琳*,杨其洪,邓杨涛,张世全
第一作者单位:四川大学数学学院,中国
第一通讯单位:上海交通大学巴黎卓越工程师学院,中国
期刊名:Nuclear Science and Engineering
期刊月份:2023年9月

01
研究背景
在核反应堆工程领域,预测中子在整个反应堆堆芯中如何分布是至关重要的,同时也是一个非常困难的问题。在实际工程应用中,中子的行为是用中子扩散方程来模拟的。近年来,深度学习的飞速发展为求解中子扩散方程问题打开了一扇新的大门。为了推进深度学习在实际工程问题上的应用,以及基于安全分析和经济效益的考虑,针对已有的科学机器学习模型在中子扩散方程上进行不确定性分析是十分必要的。
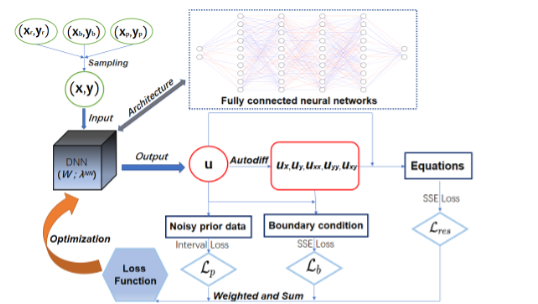
图1:增加了区间损失函数的DEPINN的计算流程图
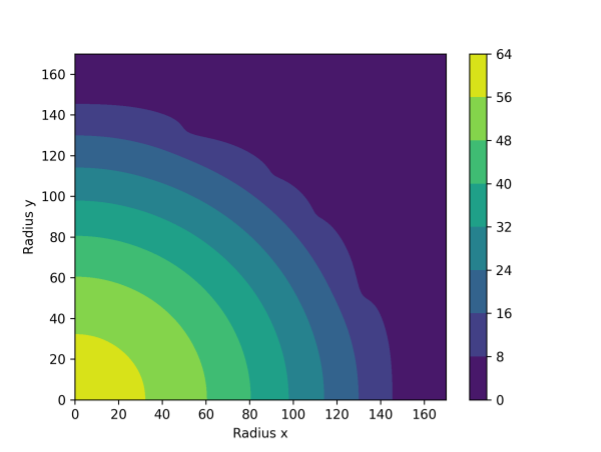
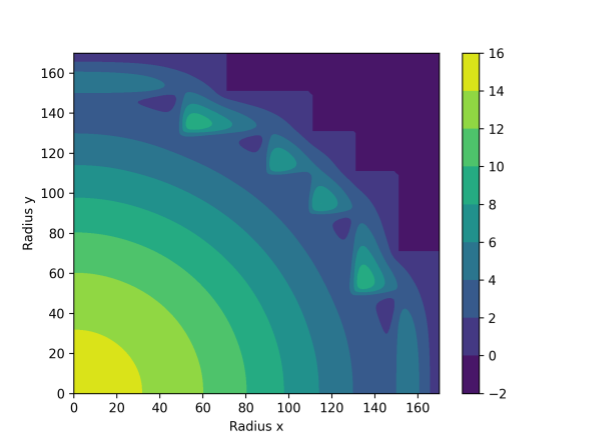
图1:神经网络对2D IAEA benchmark problem
的通量预测结果。
02
科研内容
上海交通大学巴黎卓越工程师学院的龚禾林团队和四川大学数学学院的贺巧琳,张世全团队系统性地分析Data-enabled Physics-informed Neural Network(DEPINN)在中子扩散方程上的鲁棒性。从改进的角度,提出了基于噪声先验数据项的区间损失函数,采用了自适应权重的方法,同时给出了相关的严格数学证明。并且在数值实验中从期望、置信区间和均方误差等不同角度对比其性能,证明了其有效性。这将助力深度学习框架进一步地应用到实际核物理工程问题当中,该方法本身具有很强的创新性和拓展性。该成果“On the uncertainty analysis of the data-enabled physics-informed neural network for solving neutron diffusion eigenvalue problem”发表在“Nuclear Science and Engineering”上(IF1.9,JCR Q2),该期刊是资历最老的同行评审期刊之一,被广泛认为是有关核科学工程的优质信息来源,2022年总刊文量仅115篇。
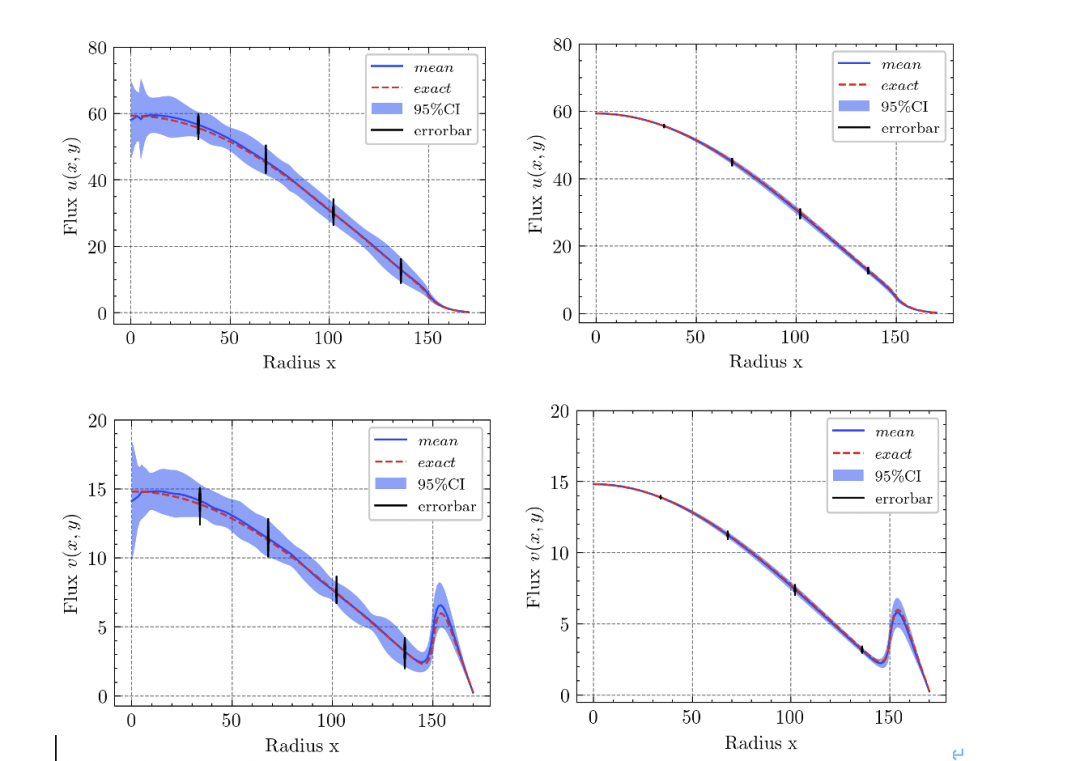
图3:区间损失函数(右)与SSE损失函数(左)的对比,大大增加了鲁棒性。
该团队在结合神经网络和核物理反应堆堆芯设计的相关研究仍然处在世界前沿,这项工作不仅推动了深度学习在实际工程问题的应用,同时也为后续编写工业软件等工作奠定了新的基石。相关工作得到了国家自然科学基金项目(No.11971020,上海市自然科学基金(No.23ZR1429300)和中核集团创新基金(领创基金)的支持。
美国核学会Twitter


近年来,上海交通大学巴黎卓越工程师学院的龚禾林团队致力于AI for Science面向工程应用的前沿研究,针对基于神经网络方法求解中子扩散方程进行持续探索,并开展了大量的应用研究,取得了丰硕成果。该系列研究与四川大学数学学院的贺巧琳,张世全团队合作完成,相关研究见:
AISEA: AI for Science with Engineering Applications(https://aisea.readthedocs.io/en/latest/)
1. Yu Yang, Helin Gong, Shiquan Zhang, Qihong Yang, Zhang Chen, Qiaolin He, Qing Li, A data-enabled physics-informed neural network with comprehensive numerical study on solving neutron diffusion eigenvalue problems, Annals of Nuclear Energy. 2023, 183: 109656,
2.Yu Yang, Helin Gong, Qiaolin He, Qihong Yang, Yangtao Deng and Shiquan Zhang, On the uncertainty analysis of the data-enabled physics-informed neural network for solving neutron diffusion eigenvalue problem, Nuclear Science and Engineering, 2023.
3. Qihong Yang, Yangtao Deng, Yu Yang, Qiaolin He, Shiquan Zhang, Neural Networks Based on Power Method and Inverse Power Method for Solving Linear Eigenvalue Problems, Computers & Mathematics with Applications, Volume 147, 1 October 2023, Pages 14-24.
4. Qihong Yang, Yu Yang, Yangtao Deng, Qiaolin He, Helin Gong, Shiquan Zhang, A Physics-Constrained Neural Network for Solving Discontinuous Interface K-eigenvalue Problem with Application to Reactor Physics, Nuclear Science and Techniques, accepted for publishing, 2023.

作者介绍
第一作者
/杨宇/
博士一年级
第二作者、通讯作者
/龚禾林/
巴黎卓越工程师学院副教授


END
文案供稿 | 龚禾林


speit2013
http://speit.sjtu.edu.cn/









